資料實用性評測
衡量合成資料在機器學習任務中的表現,以判斷其是否能有效取代原始資料。
選擇適合的任務類型
效用評測任務的選擇取決於:
資料特性
- 全為數值特徵:最適合迴歸或聚類任務
- 混合類別與數值:適合任何任務類型
- 有目標變數:分類或迴歸任務
- 無目標變數:僅能進行聚類任務
領域知識
考慮資料的預期用途:
- 預測建模:根據目標類型選擇分類或迴歸
- 模式發現:考慮聚類進行探索性分析
- 風險評估:分類任務通常提供最清晰的洞察
評測策略
雖然我們的範例資料集可以支援所有三種任務類型,您只需要選擇一個最能代表資料實用性的任務。選擇與實際使用案例最相關的任務。
共同參數
所有效用評測都共享這些基本參數:
| 參數 | 類型 | 預設值 | 說明 |
|---|---|---|---|
| method | string | 必要 | 固定值:mlutility |
| task_type | string | 必要 | 任務類型:classification、regression 或 clustering |
| experiment_design | string | domain_transfer | 實驗設計:domain_transfer 或 dual_model_control |
| random_state | integer | 42 | 隨機種子以確保可重現性 |
實驗設計策略
experiment_design 參數決定如何訓練和評估模型以評估合成資料實用性。
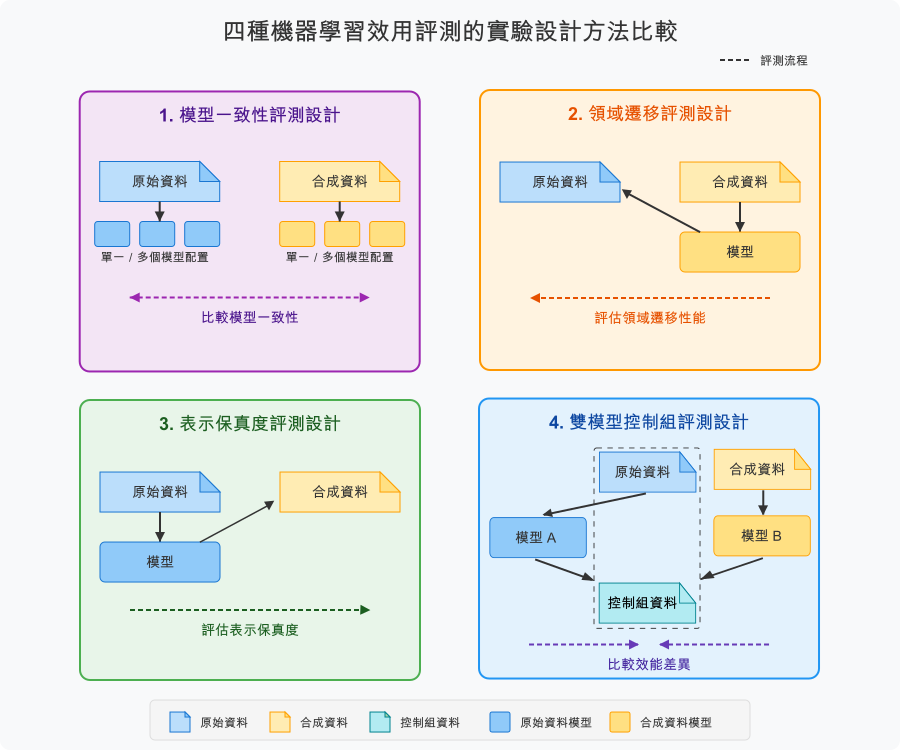
領域遷移(預設)
問題:「合成資料是否捕捉到能泛化到真實資料的基本模式?」
- 實作:在合成資料上訓練,在原始資料上測試
- 使用案例:在存取真實資料前進行模型開發
- 解釋:高效能表示強大的模式保留
- 為何預設:符合 NIST SP 800-188 對合成資料驗證的指引
雙模型控制組
問題:「合成資料能否達到與原始資料相當的模型效能?」
- 實作:在原始和合成資料上訓練獨立模型,在控制資料集上測試兩者
- 使用案例:驗證合成資料作為原始資料的替代品
- 解釋:小效能差距(< 10%)表示高實用性
模型一致性(未支援)
問題:「合成資料是否導致相同的模型選擇決策?」
- 實作:使用排序相關比較模型排名
- 使用案例:AutoML 和超參數優化情境
- 解釋:高相關性(> 0.7)能夠進行可靠的模型選擇
表示保真度(未支援)
問題:「合成資料與學習的分布匹配得有多好?」
- 實作:在原始資料上訓練,在合成資料上測試
- 使用案例:驗證合成品質和分布匹配
- 解釋:高效能暗示良好的分布保留
結果評估準則
依實驗設計
領域遷移
- 使用絕對指標值(例如 ROC AUC > 0.8)
- 較高的值表示更好的泛化
雙模型控制組
- 關注模型間的指標差異
- 較小的差異(< 10%)表示更好的實用性
模型一致性(當可用時)
- 評估排序相關係數
- 值 > 0.7 表示強一致性
設定接受標準
- 預先定義標準:在評估前建立明確的標準
- 產業合作:考慮特定領域的要求
- 任務優先順序:分類任務通常提供最清晰的洞察
- 多指標聚合:需要多個指標時使用加權平均
不平衡資料處理
ROC AUC 侷限性
在高度不平衡的資料集中,ROC AUC 可能產生誤導性的樂觀結果:
範例:欺詐偵測,正例率約 3-4%
- ROC AUC:0.86-0.90(看起來很好)
- 敏感度:0.54-0.56(近半欺詐案例被遺漏)
綜合評測策略
主要指標:MCC
- 考慮所有混淆矩陣元素
- 對不平衡資料集穩健
輔助指標:PR AUC
- 聚焦於正類品質
- 少數類別 < 10% 時使用
重採樣方法
- SMOTE-ENN:用於邊界不清的雜訊資料
- SMOTE-Tomek:用於有重疊類別的較乾淨資料
參考文獻
NIST SP 800-188. (2023). De-Identifying Government Data Sets. Section 4.4.5 “Synthetic Data with Validation”
Davis, J., & Goadrich, M. (2006). The relationship between precision-recall and ROC curves. Proceedings of the 23rd International Conference on Machine Learning, 233-240. https://doi.org/10.1145/1143844.1143874
Chicco, D., & Jurman, G. (2020). The advantages of the Matthews correlation coefficient (MCC) over F1 score and accuracy in binary classification evaluation. BMC Genomics, 21(1), Article 6. https://doi.org/10.1186/s12864-019-6413-7
Saito, T., & Rehmsmeier, M. (2015). The precision-recall plot is more informative than the ROC plot when evaluating binary classifiers on imbalanced datasets. PLOS ONE, 10(3), e0118432. https://doi.org/10.1371/journal.pone.0118432